2020重庆高考数学真题(文科) 2020年重庆高考数学试卷
时间:2022-06-30人气:作者:佚名

1.已知集合A=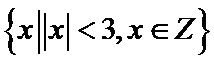 ,B=
,B=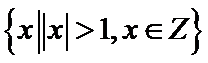 ,则
,则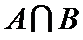 =
=
A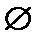
B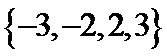
C
D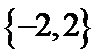
2. 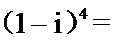
A-4
B4
C-4i
D4i
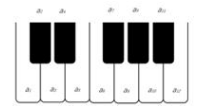
3.如图,将钢琴上的12个键依次记为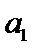 ,
,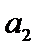 ,…,
,…,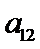 .设
.设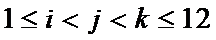 .若
.若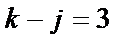 且
且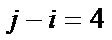 ,则称
,则称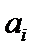 ,
,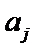 ,
,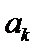 为原位大三和弦;若
为原位大三和弦;若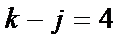 且
且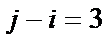 ,则称
,则称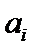 ,
, ,
,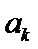 为原位小三和弦.用这12个键可以构成的原位大三和弦与原位小三和弦的个数之和为
为原位小三和弦.用这12个键可以构成的原位大三和弦与原位小三和弦的个数之和为
A5
B8
C10
D15
4.在新冠肺炎疫情防控期间,某超市开通网上销售业务,每天能完成1200份订单的配货,由于订单量大幅增加,导致订单积压,为解决困难,许多志愿者踊跃报名参加配货工作,已知该超市某日积压500份订单未配货,预计第二天的新订单超过1600份的概率为0.05。志愿者每人每天能完成50份订单的配货,为使第二天完成积压订单及当日订单的配货的概率不小于0.95,则至少需要志愿者
A10名
B18名
C24名
D32名
5.已知单位向量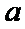 ,
,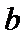 的夹角为60°,则在下列向量中,与
的夹角为60°,则在下列向量中,与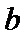 垂直的是
垂直的是
A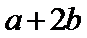
B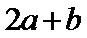
C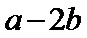
D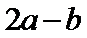
6.记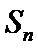 为等比数列{
为等比数列{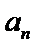 }的前
}的前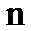 项和. 若
项和. 若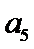 -
-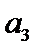 =12,
=12,  -
-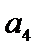 =24,则
=24,则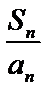 =
=
A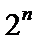 -1
-1
B2-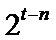
C2-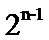
D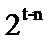 -1
-1
7. 执行右面的程序框图,若输入的k=0,a=0,则输出的k为:
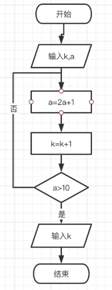
A2
B3
C4
D5
8.若过点(2,1)的圆与两坐标轴都相切,则圆心到直线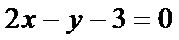 的距离为
的距离为
A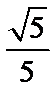
B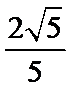
C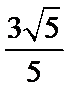
D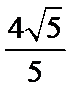
9.设O为坐标原点,直线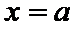 与双曲线C:
与双曲线C: (a>0,b>0)的两条渐近线分别交于D,E两点,若
(a>0,b>0)的两条渐近线分别交于D,E两点,若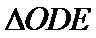 的面积为8,则C的焦距的最小值为
的面积为8,则C的焦距的最小值为
A4
B8
C16
D32
10.设函数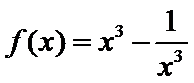 ,则
,则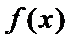
A是奇函数,且在(0,+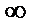 )单调递增
)单调递增
B是奇函数,且在(0,+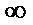 )单调递减
)单调递减
C是偶函数,且在(0,+ )单调递增
)单调递增
D是偶函数,且在(0,+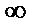 )单调递减
)单调递减
11
已知△ABC是面积为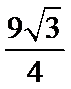 的等边三角形,且其顶点都在球
的等边三角形,且其顶点都在球
试卷全文如下







最新文章

9月份入园的新生,7、8两个月体检合格有效,其他时间入园的,入园前1个月内体检有效。厦门市妇幼保健院和全市各区妇幼保健院入园体检报告全市通用。
(359)人喜欢2024-10-07
2024年无为市中招第一批次普通高中录取分数线已经公布,小编给大家整理出来了,详见正文。
(350)人喜欢2024-10-07
2024年7月13日中午12:00开始,芜湖中考各批次可以查询录取结果,详见正文。
(356)人喜欢2024-10-07
1、平行志愿abc是第一志愿,招考办在投档考生时,要首先投档第一志愿填报的三个学校。如果你没有被第一志愿的abc三个学校录取,就可以参加第二平行志愿的abcde学校的投档录取。2、填报志愿时,第一志愿的三个学校可以填报与
(330)人喜欢2024-10-07

9月份入园的新生,7、8两个月体检合格有效,其他时间入园的,入园前1个月内体检有效。厦门市妇幼保健院和全市各区妇幼保健院入园体检报告全市通用。
(359)人喜欢2024-10-07
2024年无为市中招第一批次普通高中录取分数线已经公布,小编给大家整理出来了,详见正文。
(350)人喜欢2024-10-07
2024年7月13日中午12:00开始,芜湖中考各批次可以查询录取结果,详见正文。
(356)人喜欢2024-10-07
1、平行志愿abc是第一志愿,招考办在投档考生时,要首先投档第一志愿填报的三个学校。如果你没有被第一志愿的abc三个学校录取,就可以参加第二平行志愿的abcde学校的投档录取。2、填报志愿时,第一志愿的三个学校可以填报与
(330)人喜欢2024-10-07









